The one-more-re-nightmare compiler
Table of Contents
one-more-re-nightmare is a pretty fast regular expression engine. The most recent versions use a new technique for producing Mealy machines, and benefit greatly from SIMD-accelerated substring search.
However, I had initially started programming one-more-re-nightmare to study outside of university classes on automata, since the classes moved very slowly, and did not expect to produce a fast regular expression engine. But one does not simply write a compiler. And one does not simply write a compiler which allows them to make graphs like this:
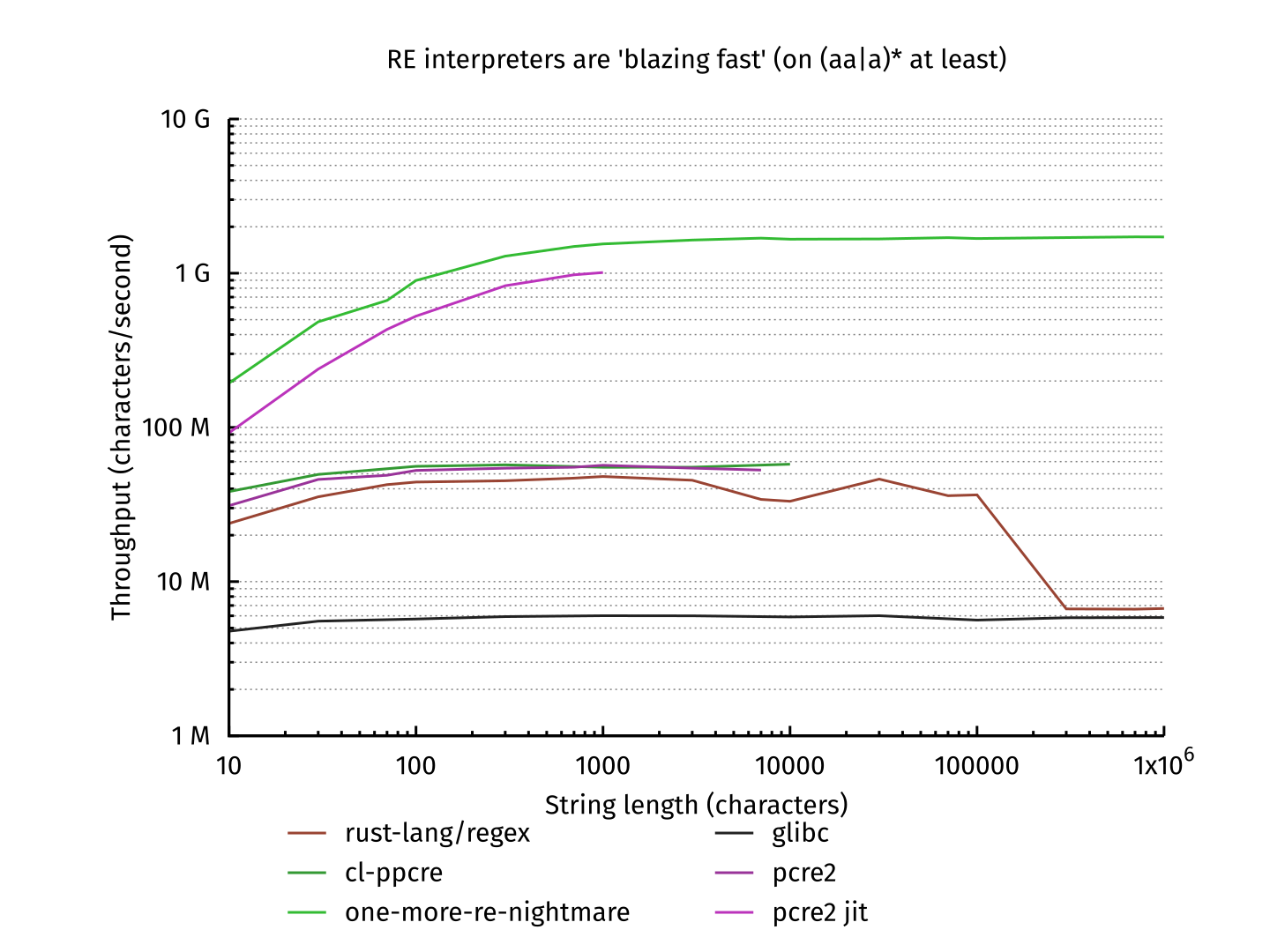
So, how does one get in such a situation, and how does one-more-re-nightmare run that fast?
Before one-more-re-nightmare
cl-ppcre
Before there was one-more-re-nightmare, there was cl-ppcre. cl-ppcre had been considered to be reasonably fast, and an exhibit of being able to compile at runtime in Common Lisp. The book Let over Lambda claims:
With CL-PPCRE, the technical reason for the performance boost is simple: Common Lisp, the language used to implement CL-PPCRE, is a more powerful language than C, the language used to implement Perl. When Perl reads in a regular expression, it can perform analysis and optimisation but eventually the regular expression will be stored into some sort of C data structure for the static regular expression engine to use when it attempts the matching. But in Common Lisp—the most powerful language—it is essentially no more difficult to take this regular expression, convert it into a lisp program, and pass that lisp program to the optimising, native-code lisp compiler used to build the rest of your lisp system.
While the claims are all true, they have nothing to do with cl-ppcre! cl-ppcre just produces a chain of closures representing the regular expression. I could believe that it was faster than Perl at the time, but it is not as fast as actually producing native code from a regular expression, such as what PCRE2 does with a bespoke JIT compiler. Still, if it was so fast for its time, it would be nice to implement a new engine which did what people thought cl-ppcre did.
Regular type expressions
I got the idea to use derivatives from a wise guy called Gilbert Baumann, but I had encountered them before while watching the 2019 European Lisp Symposium from a (roughly 20 megametre) distance. Without going into too much depth into derivatives, as I mostly want to focus on new stuff, a derivative of a regular expression (or any language) is the language you would get by removing a character off the front of the language. For example, \(\delta_a (ab)\ast\) (read as "the derivative of \((ab)\ast\) with respect to \(a\)) is \(b(ab)\ast\), as one must match the latter expression after matching the character \(a\) in order to match the original expression.
At the time of ELS 2019, I knew a guy who knew a guy who knew a guy
who was working on regular type expressions, and his implementation
used derivatives and a large tagbody form to run a deterministic
finite automaton over a sequence. This design seemed fairly simple to
implement, and thus the first compiler was born.
The old compiler
The history of one-more-re-nightmare is roughly dividable into the old and new compilers. The old compiler was developed in June 2020 through August 2020. The compiler was implemented by porting functions from Regular-expression derivatives reexamined into Lisp, which came somewhat naturally using a pattern matching library and custom patterns for all the structures involved. For example, the derivative function looked like:
(defun derivative (re set) "Compute the derivative of a regular expression with regards to the set (i.e. the regular expression should be matched after a character in the set is matched)." (trivia:ematch re ((empty-string) (empty-set)) ((literal matching-set) (if (set-null (set-intersection matching-set set)) (empty-set) (empty-string))) ((join r s) (if (nullable r) (either (join (derivative r set) s) (derivative s set)) (join (derivative r set) s))) ((kleene r) (join (derivative r set) (kleene r))) ...))
The only tricky part was that I was not sure how to translate the deterministic finite automaton construction code (on page 7), as the notation made no sense to me. But it was simple to write a regular expression interpreter, which repeatedly took derivatives of regular expressions while scanning, and so comparing execution traces from the interpreter and from manually following the DFA sufficed to get a working function which produced DFAs.
It was then fairly straightforward to write code which would produce
Lisp code from a DFA, based on the code produced by that
implementation of regular type expressions. The only difference was
that I had to scan over a vector, which requires an index variable,
and I had already come up with the name "One More RE Nightmare", so I
decided to use a prog form instead of tagbody, which is basically
entirely cosmetic, but fits the pun.1
The performance of the original compiler was…fine. Nothing amazing,
but it was about 13.4 times as fast as cl-ppcre on one of the few
tests I dared to compile, which was the expression ab|ac. It could
scan about 550 megacharacters per second,2 which seemed
pretty good given that I was executing a very branch-heavy state
machine. In comparison, a simple hand-coded recogniser3
for ab|ac was only a little faster, scanning 660 megacharacters per
second.
As time went on, I wanted something else to implement in my regular expression engine, and submatching seemed like a good choice. By then, the university class on automata finally got around to producing state machines, so I asked the teacher if he had any ideas about submatching, but he did not have any. However, Gilbert had given me access to a draft of a paper on producing Mealy machines with tag assignments, which can be used to implement submatching, and I attempted to implement them to no avail. He also wrote about some other tricks, and accidentally helped me show myself that there were some bugs around handling Kleene closures, which convinced me that I needed a new compiler.
The new compiler
The new compiler has been developed since April of 2021. The main features of the new compiler are that submatching and matching Kleene closures actually work, and these are accomplished by using Mealy machines rather than just discrete finite automata.
Mealy machines
A DFA simply consumes a stream of events, and it either stops on an accepting state or not. A Mealy machine outputs some signal, such as tag assignments in our case, while transitioning between states. Such assignments simply copy a position from a register, which is either the current position or another tag register, to another tag register. We write submatches in « », so that they can't be confused for ( ) which are merely used to work around operator precedence. For example, here is a simple Mealy machine which matches \(«ab»\):
We have annotated each transition with the assignments to produce, as well as the characters that must be read to take a transition. Accepting states are also annotated with an "exit map", which contains a set of registers that should be output, as well as some final assignments to make. We also assume that assignments are performed before advancing across the sequence to match, and so read old positions. For example, this machine should produce \(start = 0, end = 2\) if matching the string \(ab\).
Of course, this is quite a simple machine, and more interesting regular expressions have a certain sort of ambiguity, in that we do not know which registers should appear in future results at a given state, but we need to emit assignments already. The key trick is to replicate registers when such ambiguity exists, and keep the registers around until we can tell when which registers will be used for submatching results. For example, \(\delta_a (a[A \leftarrow position]bc + ab[A \leftarrow position]d) = [A]bc + b[A_2 \leftarrow position]d\).
That said, we use a slight variation on this approach, where it is assumed that such ambiguity is only produced as part of computing derivatives, so most replication is avoided by a few simple special cases. This assumption holds for any real regular expression syntax, as submatches only produce assignments to a given register in one location, and I call this style of tagged regular expression an affine tagged regular expression, as I am terrible at coming up with catchy names. Duplication tends to be common when handling Kleene closures, and it is usually in pretty messy derivatives (such as those for \(«a + aa»\ast\)) just to keep you awake.
In order to ensure that a finite automaton can be constructed, it is also necessary to remove duplicate subexpressions which only differ in registers used. For example, the regular expression \([A \leftarrow a] c + [B \leftarrow b] c\) should be rewritten to \([A \leftarrow a] c\), as only the assignment to \(A\) will be observed under our semantics.
Backtracking but not "backtracking"
Registers are also used in order to correctly implement Kleene closures. Suppose we have a regular expression \((abc)*\), and we are searching over the string \(abcab\). While the whole string \(abcab\) does not match the regular expression, we are usually interested in substrings which match, and so a regular expression engine should report that the substring \(abc\) still matches. In order to track such matches even when we have gone past them, we more or less wrap the regular expression in a submatch without any name that is visible to the user, and recall the last successful matching position if there is one when we fail to match the entire string.
As we use a DFA, we don't "backtrack" in the sense that a regex engine with a NFA does. But the naïve approach to handling failure is to restart everything starting from the next character after the previous start, which produces a \(\mathcal{O}(n^2)\) runtime. We can instead further avoid any "backtracking" past the end of a match by transforming our DFA. Typically, one focuses on machines which just match one string, but we would prefer a machine which just finds a matching substring while continually advancing through the sequence to scan. We might as well call this behaviour scanning (or alternately grepping, as the notation for this function on a regular expression implies). A scanning machine for \(ab\) could look like:
I don't have the guts to derive such a machine by hand, so I use a function in one-more-re-nightmare which lets me print generated DFAs.
The implementation of a scanning function is simple. We'll write a scanner which is currently looking through some expressions \(e\) and has a "prototype" expression \(p\) as \(\gamma[e, p]\). I had mentioned replicating registers in order to handle ambiguity; we use a function called \(\text{dup}\) to show where registers have to be replicated. Now the rule for a derivative of a scanner is:
\[\delta_a \gamma[e, p] = \gamma[(\delta_a e) + \text{dup}(p), p]\]
Or, in other words, we set up another clone of the prototype expression to scan at each character. That might sound like a lot of clones, but most clones die young,4 as they usually don't match even the first character of most expressions to random places in the string.
Using grep machines and paying attention to register allocation increased throughput to 1.25 gigacharacters a second. With regards to register allocation: we call a "continuation" function with matching results, and calling a function requires spilling registers. It appears that register allocators in various Common Lisp compilers (I mostly test on SBCL and Clozure) prefer it when there is only one function call in the generated code, rather than a function call for each accepting state, and the reduced number of spills and unspills improves performance.
SIMD
Another feature of the old compiler was that it could search for
constant prefixes of regular expressions using the
Boyer-Moore-Horspool algorithm, which was often faster than running
the normal DFA. Suppose we are scanning for the regular expression
c[ad]+r. We could separate this into the concatenation of a
constant string c[ad] and a regular expression [ad]*r, as GNU
grep apparently does, and then only run a DFA simulation if we find a
match for the constant string.
Constant strings are apparently common enough that one should always
look for them. The Usenix paper on Hyperscan reports 87 to 94% of
regular expressions used in intrusion detection systems have constant
strings; but Hyperscan can look for a string anywhere in the
expression, whereas we are stuck with prefixes. But there are
presumably enough grammars where all constants are prefixes and
suffixes, so we are not at a huge loss with this design decision.
Instead, we allow for "constant" strings to contain any sets of
characters, so ab|ac for example has a prefix a[bc].
We currently represent a set of characters as a union of some
half-open ranges. For example, the character set in the regular
expression [a-ce] is represented as \([97, 100) \cup [101,
102)\). This representation works well to produce good code for
dispatching on characters, but we are hampered by the lack of
instructions in some SIMD instruction sets, such as SSE2 and
AVX2. Typically, we might generate code representing the expression
\((97 \leq c < 100) \lor (101 = c)\), but these instruction sets only
have instructions for \(<\) and \(=\)! Worse, using a signed or unsigned
representation matters for \(<\), and these instruction sets only
provide signed comparisons.
In the case of scanning a Unicode string, we fortunately do not need to worry about signs, as Unicode codepoints do not get close to exceeding \(2^{31}\) (yet) and so all codepoints are the same under both signed and unsigned interpretations. As such, we only need the following rewrite rules to translate \(\leq\):
\begin{align*} 0 \leq c &\equiv \top\>\> \text{[as c cannot be negative]}\\ x \leq c &\equiv (x - 1) < c \end{align*}
However, we still want to support scanning over byte vectors (and
simple-base-string, which tends to use a byte per character, but
only can contain ASCII characters), so we need to handle signed
comparisons somehow. We must map elements from \([0, 256)\) to \([-128,
128)\) while preserving the behaviour of \(<\). The easiest mapping
function is probably \(\lambda x. x - 128\), which is what we use.
A performance comparison with ab|ac is unfair, as the entire regular
expression is a constant prefix, by our definition. But we can scan
ab|ac at 5.5 gigacharacters a second, using a normal Unicode string,
which is about 4.6 times as fast as scalar code, and we can scan at 18
gigacharacters a second over a simple-base-string! Another
interesting benchmark is scanning Xorg.log for resolutions with the
regular expression "[0-9]+x[0-9]+", which yields the following
results with various regular expression engines:
| Engine | Throughput |
|---|---|
| CL-PPCRE | 414Mchar/s |
| Scalar one-more-re-nightmare | 1.0Gchar/s |
| Hyperscan | 1.5Gchar/s |
| Rust regex | 4.2Gchar/s |
| AVX2 one-more-re-nightmare | 11.2Gchar/s |
It appears that one-more-re-nightmare might be unique in capturing the
"[0-9] prefix as two sets of characters; I am aware that the Rust
regex library can search for a single byte, a constant string or an
Aho-Corasick automaton, but not a simpler sequence of sets of
characters.
What's next?
It might be useful to go more Hyperscan-ny and allow for finding
constant strings and simpler expressions anywhere. For example, we are
much less impressive over the regular expression [0-9]+x[0-9]+, with
the following results:
| Engine | Throughput |
|---|---|
| CL-PPCRE | 51.3Mchar/s |
| AVX2 one-more-re-nightmare | 354Mchar/s |
| Scalar one-more-re-nightmare | 365Mchar/s |
| Hyperscan | 427Mchar/s |
| Rust regex | 668Mchar/s |
However, if we recognised the trigram [0-9]x[0-9] that must appear
in the middle of a matching substring, then we could just scan for
[0-9]* on either side to match the entire regular expression, and
recover the benefits of SIMD searching. (Hyperscan does not seem to
have spotted this optimisation, so using it as an adjective is
ironic in hindsight.)
As generating DFAs is fundamentally a \(\mathcal{O}(2^n)\) process, and our scanning function can also increase DFA size, it also might be useful to look into "hybrid" constructions. For example, just remembering \(n\) clones for some small \(n\) would avoid backtracking for \(n\) characters, which would produce a simpler DFA while still reducing the backtracking somewhat.
A POSIX regular expression parser would probably be more useful,
rather than a parser for a syntax I came up with by reading papers
which used a more "mathematical" notation. But I do like the idea of
using «» for submatches, rather than (), since (?:blah) (to not
match) looks awkward. Everyone has compose keys, right?
Conclusion
So, more or less, one-more-re-nightmare does what people think the original regular expression nightmare (cl-ppcre) does. In order to achieve this goal, it does not do everything cl-ppcre does: backreferences are out of the question, and lookahead/behind is still an open problem. But there is hopefully enough of a regular expression engine to be useful.
Before I forget, the entire one-more-re-nightmare library still only sits at a mere 1,848 lines of code. The small size of the library is presumably due to using pattern matching for functions and rewrite rules, and to using the Common Lisp compiler as a backend for native code generation.
It was recently claimed that techniques for writing a fast grep have converged. Based on preliminary results with running a real compiler, and now SIMD, I respectfully disagree. The game is still on; and let the best scanner win!
Footnotes:
The name is of course a reference to One More Red Nightmare.
Most Common Lisp implementations store characters as decoded 32-bit integers, as strings are a special case of vectors and thus \(\mathcal{O}(1)\) access would be expected.
I compare with this recogniser:
(defun ab-ac (string) (declare (optimize (speed 3) (safety 0)) ((simple-array character 1) string)) (loop for p below (1- (length string)) when (and (char= (char string p) #\a) (or (char= (char string (1+ p)) #\b) (char= (char string (1+ p)) #\c))) collect p))
The generational hypothesis for regular expressions?